On the benefits of sorted paths
I had the pleasure to attend PGDay UK last week – a very nice event, hopefully I’ll have the chance to come back next year. There was plenty of interesting talks, but the one that caught my attention in particular was Performace for queries with grouping by Alexey Bashtanov.
I have given a fair number of similar performance-oriented talks in the past, so I know how difficult it is to present benchmark results in a comprehensible and interesting way, and Alexey did a pretty good job, I think. So if you deal with data aggregation (i.e. BI, analytics, or similar workloads) I recommend going through the slides and if you get a chance to attend the talk on some other conference, I highly recommend doing so.
But there’s one point where I disagree with the talk, though. On a number of places the talk suggested that you should generally prefer HashAggregate, because sorts are slow.
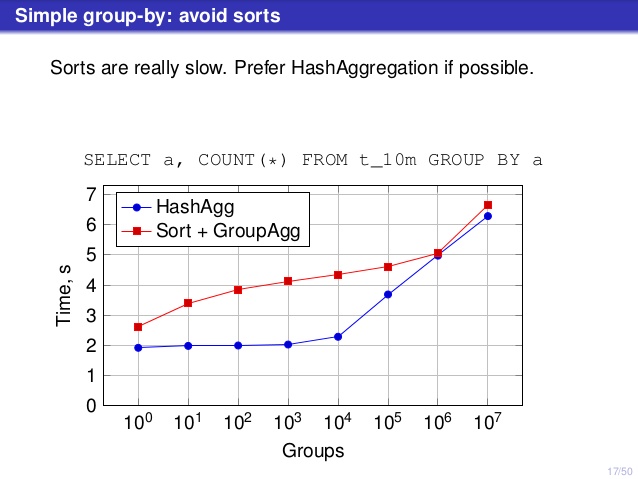
I consider this a bit misleading, because an alternative to HashAggregate is GroupAggregate, not Sort. So the recommendation assumes that each GroupAggregate has a nested Sort, but that’s not quite true. GroupAggregate requires sorted input, and an explicit Sort is not the only way to do that – we also have IndexScan and IndexOnlyScan nodes, that eliminate the sort costs and keep the other benefits associated with sorted paths (especially IndexOnlyScan).
Let me demonstrate how (IndexOnlyScan+GroupAggregate) performs compared to both HashAggregate and (Sort+GroupAggregate) – the script I’ve used for the measurements is here. It builds four simple tables, each with 100M rows and different number of groups in the “branch_id” column (determining the size of the hash table). The smallest one has 10k groups
-- table with 10k groups create table t_10000 (branch_id bigint, amount numeric); insert into t_10000 select mod(i, 10000), random() from generate_series(1,100000000) s(i);
and three additional tables have 100k, 1M and 5M groups. Let’s run this simple query aggregating the data:
SELECT branch_id, SUM(amount) FROM t_10000 GROUP BY 1
and then convince the database to use three different plans:
1) HashAggregate
SET enable_sort = off;
SET enable_hashagg = on;
EXPLAIN SELECT branch_id, SUM(amount) FROM t_10000 GROUP BY 1;
QUERY PLAN
----------------------------------------------------------------------------
HashAggregate (cost=2136943.00..2137067.99 rows=9999 width=40)
Group Key: branch_id
-> Seq Scan on t_10000 (cost=0.00..1636943.00 rows=100000000 width=19)
(3 rows)
2) GroupAggregate (with a Sort)
SET enable_sort = on;
SET enable_hashagg = off;
EXPLAIN SELECT branch_id, SUM(amount) FROM t_10000 GROUP BY 1;
QUERY PLAN
-------------------------------------------------------------------------------
GroupAggregate (cost=16975438.38..17725563.37 rows=9999 width=40)
Group Key: branch_id
-> Sort (cost=16975438.38..17225438.38 rows=100000000 width=19)
Sort Key: branch_id
-> Seq Scan on t_10000 (cost=0.00..1636943.00 rows=100000000 ...)
(5 rows)
3) GroupAggregate (with an IndexOnlyScan)
SET enable_sort = on;
SET enable_hashagg = off;
CREATE INDEX ON t_10000 (branch_id, amount);
EXPLAIN SELECT branch_id, SUM(amount) FROM t_10000 GROUP BY 1;
QUERY PLAN
--------------------------------------------------------------------------
GroupAggregate (cost=0.57..3983129.56 rows=9999 width=40)
Group Key: branch_id
-> Index Only Scan using t_10000_branch_id_amount_idx on t_10000
(cost=0.57..3483004.57 rows=100000000 width=19)
(3 rows)
Results
After measuring timings for each plan on all the tables, the results look like this:
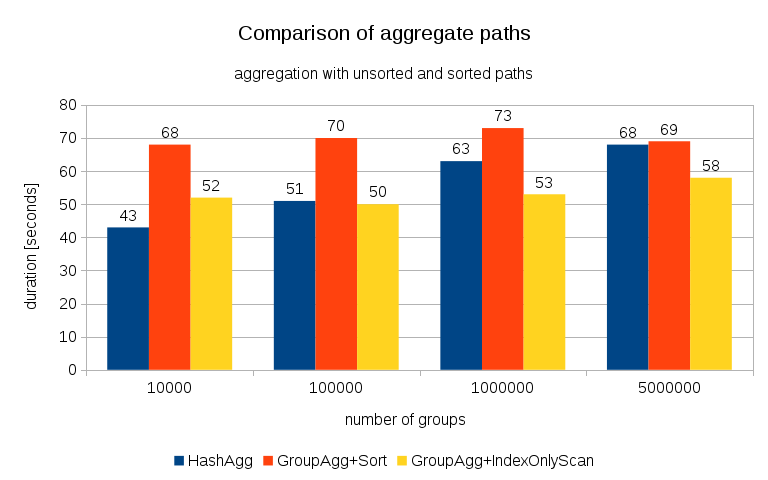
For small hash tables (fitting into L3 cache, which is 16MB in this case), HashAggregate path is clearly faster than both sorted paths. But pretty soon GroupAgg+IndexOnlyScan gets just as fast or even faster – this is due to cache efficiency, the main advantage of GroupAggregate. While HashAggregate needs to keep the whole hash table in memory at once, GroupAggregate only needs to keep the last group. And the less memory you use, the more likely it’s to fit that into L3 cache, which is roughly an order of magnitude faster compared to regular RAM (for the L1/L2 caches the difference is even larger).
So although there’s a considerable overhead associated with IndexOnlyScan (for the 10k case it’s about 20% slower than the HashAggregate path), as the hash table grows the L3 cache hit ratio quickly drops and the difference eventually makes the GroupAggregate faster. And eventually even the GroupAggregate+Sort gets on par with the HashAggregate path.
You might argue that your data generally have fairly low number of groups, and thus the hash table will always fit into L3 cache. But consider that the L3 cache is shared by all processes running on the CPU, and also by all parts of the query plan. So although we currently have ~20MB of L3 cache per socket, your query will only get a part of that, and that bit will be shared by all nodes in your (possibly quite complex) query.
Update 2016/07/26: As pointed out in the comments by Peter Geoghegan, the way the data was generated probably results in correlation – not the values (or rather hashes of the values), but memory allocations. I’ve repeated the queries with properly randomized data, i.e. doing
insert into t_10000 select (10000*random())::bigint, random() from generate_series(1,100000000) s(i);
instead of
insert into t_10000 select mod(i, 10000), random() from generate_series(1,100000000) s(i);
and the results look like this:
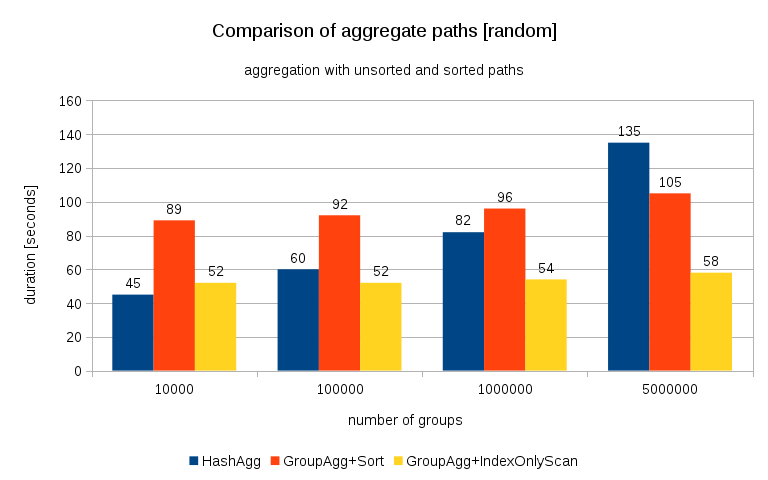
Comparing this with the previous chart, I think it’s pretty clear the results are even more in favor of sorted paths, particularly for the data set with 5M groups. The 5M data set also shows that GroupAgg with an explicit Sort may be faster than HashAgg.
Summary
While HashAggregate is probably faster than GroupAggregate with an explicit Sort (I’m hesitant to say it’s always the case, though), using GroupAggregate with IndexOnlyScan faster can easily make it much faster than HashAggregate.
Of course, you don’t get to pick the exact plan directly – the planner should do that for you. But you affect the selection process by (a) creating indexes and (b) setting work_mem. Which is why sometimes lower work_mem (and maintenance_work_mem) values result in better performance.
Additional indexes are not free, though – they cost both CPU time (when inserting new data), and disk space. For IndexOnlyScans the disk space requirements may be quite significant because the index needs to include all the columns referenced by the query, and regular IndexScan would not give you the same performance as it generates a lot of random I/O against the table (eliminating all the potential gains).
Another nice feature is the stability of the performance – notice how the HashAggregate timings chance depending on the number of groups, while the GroupAggregate paths perform mostly the same.





Unrelated to your point, but if the query uses NeuStar’s pg-hll extension (fast approximate COUNT DISTINCT using the HyperLogLog algorithm), a hash join will typically run out of memory because each HLL value consumes tens of kilobytes of RAM.
Yes, you’re right – HashAggregate is vulnerable to OOM while GroupAggregate is safe. I believe this is what Alexey meant by “if possible” in his slides.
Good analysis.
Every decade or so, a new paper comes out called “Sort vs. Hash revisited”. Right now, current hardware trends have made the pendulum swing in favor of sort (although, obviously both approaches to aggregation have strengths and weaknesses on any particular CPU, as you describe).
You say “While HashAggregate is probably faster than GroupAggregate with an explicit Sort (I’m hesitant to say it’s always the case, though)”. As you suspect, there are plenty of cases where GroupAggregate is still faster. If you want to make a query like your “select branch_id, sum(amount) from t_5000000 group by 1;” example look faster with a GroupAggregate, it’s quite possible. Just make sure that the table is in no particular order when generating data, to make the HashAggregate less capable of exploiting natural locality. The same tuples can be used, but their order in the heap/table should be randomized.
On my laptop, doing so makes the HashAggregate plan take about twice as long, and about 10% slower than a GroupAggregate + sort on the same reordered table. This is the cases despite the fact that the sort is an external sort, that must merged 6 runs.
When there is a preexisting correlation in physical table order to logical value order, then chances are pretty good that you have an index. When there isn’t, and when there is a large number of groupings, changes are reasonable that a GroupAggregate + sort is the better strategy overall. Recent improvements to tuplesort.c may have changed this.
Peter Geoghegan
Isn’t that pretty much the data I’ve used for the testing? Mod(i,N) wraps around, so to HashAggregate that should look pretty random thanks to the hashing, no? Yet the HashAgg does not get slower than GroupAgg+Sort.
Seems pretty well correlated to me:
“””
postgres=# select ctid, * from t_100000 limit 10;
ctid │ branch_id │ amount
────────┼───────────┼────────────────────
(0,1) │ 1 │ 0.45625233091414
(0,2) │ 2 │ 0.0573322377167642
(0,3) │ 3 │ 0.74035676009953
(0,4) │ 4 │ 0.129757477901876
(0,5) │ 5 │ 0.672162196133286
(0,6) │ 6 │ 0.933008610736579
(0,7) │ 7 │ 0.818270212970674
(0,8) │ 8 │ 0.908431205432862
(0,9) │ 9 │ 0.938376571517438
(0,10) │ 10 │ 0.64439286198467
(10 rows)
“””
Yes, the values are correlated, but not the hashes of the values. When building the hash table, it’s hashint8(branch_id) that determines the bucket, no?
The correlation I had in mind is when there are streaks of the same branch_id value, so that the hash lookup is likely to find it in L3 cache.
Well, values will repeat until a wrap-around, like this:
*** SNIP ***
(63,102) │ 9,993 │ 0.0748952180147171
(63,103) │ 9,994 │ 0.64047087309882
(63,104) │ 9,995 │ 0.64456010889262
(63,105) │ 9,996 │ 0.695730244275182
(63,106) │ 9,997 │ 0.339152801781893
(63,107) │ 9,998 │ 0.980276728514582
(63,108) │ 9,999 │ 0.452988512348384
(63,109) │ 0 │ 0.653703771997243
(63,110) │ 1 │ 0.613569085951895
(63,111) │ 2 │ 0.758732107002288
(63,112) │ 3 │ 0.672823683358729
(63,113) │ 4 │ 0.06704619852826
(63,114) │ 5 │ 0.642444666475058
*** SNIP ***
When there are more groupings than you see here, where it might matter noticeably, don’t you think that there could be a benefit because of locality of access, possibly due to the initial order of memory allocation for buckets? The effect seemed noticeable to me, although I am not an expert on hashing.
Another possible effect that I did not initially consider is the quicksort presorted input best case being continually defeated, and continually throwing away real work.
Good point! I have only considered the random access to buckets (due to the hashing), but you’re probably right that the actual data (aggregate state) will be allocated and accessed mostly sequentially.
I’ll repeat the tests with a truly randomized data set, but it’ll take a bit of time as the machine is currently tortured by someone else 😉
To be clear, I don’t think you were wrong to not make sure that the input was not at all ordered. It’s a legitimate advantage that some preexisting correlation can be exploited (this is also true for GroupAggregate + sort, but that manages to do okay with locality of access *despite* the lack of a correlation, unlike the HashAggregate case).
In short, I just think that this is a factor that’s worth noting as part of a deep technical analysis like this.
I definitely agree it’s an interesting factor. And I’d argue it actually should have been mentioned in the post – at least I should have mentioned that I believe the data is not correlated (which seems incorrect, now). So thanks for the comments, it’s why I write these blog posts.
Another interesting case is a multi-attribute GroupAggregate, where multiple text Group keys are used. Provided that the C collation was used (this is important because we lost abbreviated keys with other collations, for now), I think that such a case could also show how compelling GroupAggregate + Sort can be.
Resolving hash collisions is much more expensive there, while at the same time the sort may not be that much slower than an int4 case due to the use of abbreviated keys.
Hi, Alexey did this useful presentation to the Brighton PostgreSQL User Group.
The recording is available here https://www.youtube.com/watch?v=_IaRhLLQfQk
Cheers
Thanks for pointing out on this problem in my talk. I have probably spent too little time of my talk on GroupAggregate acting without explicit sorts — roughly only 10-20 seconds in speech, nothing on slides.
GroupAggregate surely can be fed from nodes returning sorted data, e.g IndexScan or MergeJoin, and I should have included a third line for IndexOnlyScan+GroupAgg in the line chart. However, the conditions for this method to be useful are a bit restrictive (proper indexes, low update rate and proper vacuuming, probably working on SSD, partitioned table will need Merge Append node), so unfortunately in practice it can be used not too often.
As for Sort+GroupAgg I have spent some time trying to find an example when it is faster than HashAgg — no results. Probably I should have done it on a server with a large CPU cache rather than on a very average laptop. Also sort algorithms are constantly improved (see these perfect slides by Gregory Stark https://pgconf.ru/media/2016/02/19/9%20%D0%A1%D1%82%D0%B0%D1%80%D0%BA.pdf), so the situation may change in future.
> sometimes lower work_mem (and maintenance_work_mem) values result in better performance
Sounds interesting, especially maintenance_work_mem. Is it about foreign key validation?
I wouldn’t call it a “problem in a talk” – it’s very difficult to get “everything” into a 45-minute talk, so not a big deal.
You’re right that for this to work, there need to be indexes, which means additional overhead for DML and disk space requirements. So yes, it’s a compromise. I don’t think SSDs are needed, though – the index makes it more sequential, actually.
Regarding the maintenance_work_mem – it’s not uncommon to see CREATE INDEX to complete much faster with smaller values (say 32MB is faster than 1GB), mostly thanks to the caching effects. I.e. the ability to perform the sorts faster outweights the batchning overhead.
And thanks for posting a link to Greg’s talk, really nice overview!
I noticed that the create index is influenced by maintenance_work_mem. work_mem affects the sorts when not involved in index creation.
to me it makes perfect sense as the index creation is maintenance.
cheers
Federico
I may be missing something, but I don’t think anyone suggested CREATE INDEX should use work_mem, or that it’s strange that it uses maintenance_work_mem?
The point is that with smaller maintenance_work_mem, the sort will have to create more batches (and then merge them), which adds overhead. But the smaller batches use the L2/L3 cache way better, outweighing the overhead. The same thing applies to work_mem, but work_mem affects other nodes too, where the cost of batching is much higher (e.g. HashJoin), or makes it impossible to use nodes that don’t support batching (e.g. HashAggregate). With maintenance_work_mem the effect is much clearer because it applies to DML statements that are typically much simpler (e.g. CREATE INDEX).
Sorry, my bad. I completely misunderstood what you wrote.